
L’emissione di un prestito obbligazionario necessita di una molteplicità di calcoli per determinare gli interessi maturati sul debito, le cedole in scadenza, il rateo di interesse a fine esercizio e la quota di ammortamento del “disagio su prestiti” da iscrivere annualmente in bilancio. In questo tutorial proponiamo un modello che consente, dopo l’immissione di pochi dati, di creare in automatico un piano di ammortamento del prestito obbligazionario completo di tutti i dati che devono essere contabilizzati in partita doppia. Il modello si basa su tre ipotesi, peraltro comunemente riscontrabili nella realtà di impresa:
- il prestito obbligazionario viene emesso all’inizio di uno dei dodici mesi dell’anno,
- il rimborso avviene a quote costanti annuali,
- il tasso di interesse è fisso.
Come utilizzare il modello
Per generare il piano di ammortamento del prestito obbligazionario è sufficiente compilare i dati appartenenti all’intervallo E3:E10 del foglio di calcolo.
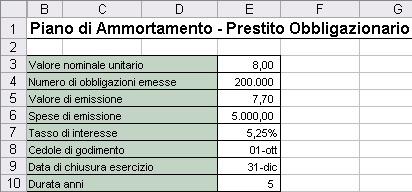
In particolare, nella cella E6 vanno inserite le spese di emissione quali ad esempio, quelle bancarie o notarili, che andranno a costituire insieme con lo “scarto” di emissione, il valore del disaggio su prestiti; nella cella E8 va indicata la data iniziale del prestito obbligazionario (che, per ipotesi, deve coincidere con il primo del mese) mentre nella cella E9 la data di fine esercizio dell’anno nel quale viene emesso il prestito (entrambe le celle sono state formattate con un formato data che non evidenzia l’anno).
Come costruire il modello
Le restanti celle del modello contengono tutte formule che andremo ad analizzare a partire dall’intervallo H3:K5.
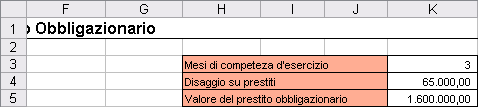
Nella cella K3 è stata utilizzata la formula
=SE(O(E9=””;E8=””);0;MESE(E9-E8))
che consente di determinare, a condizione che le celle E8 e E9 contengano dei valori, i mesi intercorrenti tra la data di fine esercizio (E9) e la data di emissione del prestito obbligazionario (E8); il risultato della formula, che nei dati riportati in figura è pari a 3 in quanto il prestito è stato emesso il primo di ottobre, sarà utilizzato per calcolare il rateo di interessi nel piano di ammortamento del prestito obbligazionario.
Per determinare il valore del disaggio su prestiti si è utilizzata nella cella K4 la formula =(E3-E5)*E4+E6 ovvero, si è moltiplicata la differenza tra il valore nominale unitario (E3) e il valore effettivo di emissione (E5) per il numero delle obbligazioni emesse (E4) e si è sommato tale valore (che rappresenta lo scarto di emissione in termini assoluti) con le spese di emissione del prestito obbligazionario (E6). Il valore del prestito obbligazionario è dato dal numero di obbligazioni emesse per il valore nominale unitario; pertanto nella cella K5 è stata utilizzata la formula =E4*E3. Proseguiamo con l’analizzare la prima parte del piano di ammortamento compresa nell’intervallo A12:G34 del foglio di calcolo.
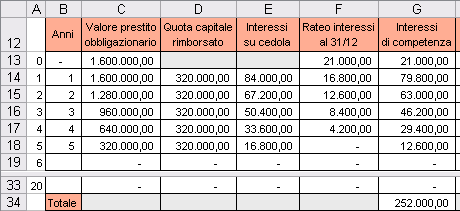
Per costruire un modello dinamico che visualizzi soltanto i dati necessari in base alla durata del prestito obbligazionario è stata utilizzata una “colonna di servizio”, la colonna A, nella quale è stata inserita una serie numerica da 0 a 20. Nella cella B13 è stata inserita la funzione
=SE(A13<=$E$10;A13;””)
e, successivamente, è stata copiata fino alla cella B33; la formula utilizzata consente la visualizzazione del valore della serie numerica fino al numero corrispondente agli anni del prestito obbligazionario (E10) mentre, le celle sottostanti visualizzeranno una “etichetta vuota”.
Per visualizzare la “quota capitale” rimborsata in ogni periodo, nella cella D14 è stata utilizzata la funzione
=SE(B14=””;0;$K$5/$E$10);
la formula restituisce la divisione tra il valore del prestito obbligazionario (contenuto nella cella K5) e la sua durata in anni (E10) soltanto se esiste un valore nella cella B14; la funzione è stata successivamente copiata verso il basso fino alla cella D33.
Per determinare il valore del prestito obbligazionario al netto della quota rimborsata annualmente, si è utilizzato nelle celle C13 un riferimento alla cella contenente il valore del prestito obbligazionario (=K5), nella cella C14 la formula =SE(B13=””;0;K5), mentre nella cella C15 la formula =SE(B15=””;0;C14-D14); quest’ultima, che consente di visualizzare il valore solo se nella corrispondente cella della colonna B è riportato un valore, è stata successivamente copiata verso il basso fino alla cella C33.
Per determinare gli interessi sulle singole cedole in scadenza si è utilizzata nella cella E14 la formula =C14*$E$7 che moltiplica il valore del prestito obbligazionario residuo (C14) per il tasso di interesse annuale (E7); la formula, costruita con un riferimento assoluto, è stata successivamente copiata fino alla cella E33. Poiché gli interessi vengono pagati alla scadenza delle cedole, a fine esercizio deve essere contabilizzato un “rateo” per la quota di interessi maturata ma non ancora versata; per calcolare tale valore si è utilizzata nella cella F13 la formula =ARROTONDA(E14*$K$3/12;2) che arrotonda a due cifre decimali la moltiplicazione tra gli interessi sulla cedola che verranno versati nell’esercizio contabile successivo (E14) e la frazione in mesi, di competenza dell’esercizio contabile in corso (K3/12); la formula è stata successivamente copiata verso il basso, sempre fino alla riga 33.
=> Scritture contabili e bilancio d’esercizio
Gli interessi di competenza si calcolano sommando gli interessi maturati dal 1 gennaio alla data di scadenza della cedola pagata durante l’esercizio e gli interessi della “nuova” cedola maturati fino al 31/12; nell’esercizio contabile nel quale viene emesso il prestito obbligazionario (esercizio 0) questi ultimi coincidono con il rateo di interessi. Pertanto nella cella G13 è stato richiamato il contenuto della cella F13 (=F13) mentre nella cella G14 è stata inserita la formula =ARROTONDA(E14*(12-$K$3)/12+F14;2). La formula, successivamente copiata fino alla cella G33, consente di sommare gli interessi sulla cedola in scadenza (E14) rapportati ai mesi di competenza ((12-K3)/12) e il rateo relativo alla nuova cedola (F14) arrotondando il risultato a due cifre decimali. Il totale degli interessi di competenza (utile per il calcolo del disaggio su prestiti) è stato calcolato nella cella G34 attraverso la funzione =SOMMA(G13:G33).
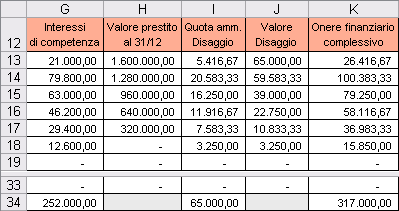
Il valore del prestito obbligazionario al 31/12, nell’esercizio contabile di emissione è pari al valore nominale dello stesso mentre, negli esercizi contabili successivi, è decurtato della “quota capitale” rimborsata; pertanto nella cella H13 è stata utilizzata la formula =C13 (che, a sua volta, fa riferimento alla cella K5 relativa al valore nominale del prestito obbligazionario) mentre, nella cella H14 è stata inserita la formula =C14-D14 (quest’ultima formula è stata copiata verso il basso fino alla cella H33).








