


Il rimborso di un prestito può avvenire con differenti modalità, che dipendono principalmente dalla composizione della quota capitale e della quota interessi delle rate; i metodi più utilizzati per i prestiti alle imprese sono due: oltre al metodo a “rate costanti“, esiste quello a “quote di capitale costanti” che proponiamo in questo tutorial, attraverso un modello già pronto all’uso. Con questo metodo, la rata del prestito è inizialmente alta e tende a scendere nel tempo in quanto gli interessi da corrispondere vengono calcolati, rata dopo rata, sul capitale residuo da restituire.
=>Scarica il modello di calcolo
Come utilizzare il modello
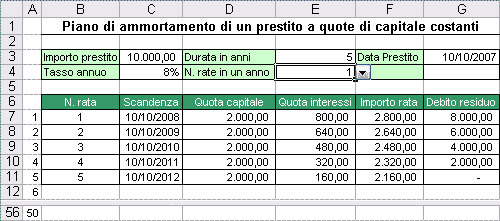
Il modello è semplice da utilizzare in quanto richiede l’inserimento di solo cinque dati.Nella cella C3 deve essere riportato l’importo del capitale ottenuto in prestito, nella cella C4 il tasso di interesse annuale (che per ipotesi è fisso per tutta la durata del prestito), nella cella E3 la durata in anni del prestito, nella cella E4 deve essere selezionato dall’elenco a discesa il numero di rate da rimborsare in un anno (se le rate sono annuali si seleziona 1, se le rate sono semestrali si seleziona 2, se quadrimestrali si seleziona 3, e così via) e nella cella G3 deve essere indicata la data di stipulazione del contratto a partire dalla quale viene concesso il prestito (tale data consentirà di calcolare le scadenze delle singole rate).
Al termine dell’inserimento dei dati viene generato automaticamente il piano di ammortamento a partire dalla riga 7 del foglio di calcolo.
Come costruire il modello
L’elenco a discesa, inserito nella cella E4 per evitare l’immissione di un valore numerico non adeguato, è stato creato utilizzando il comando Convalida del menu Dati e digitando nella casella di testo Origine, presente all’interno della scheda Impostazioni della finestra Convalida dati, i valori numerici 1, 2, 3, 4, 6 e 12 separati da un punto e virgola. Per creare un piano di ammortamento flessibile, che modifichi la sua lunghezza in base al numero di rate, è stata inserita una serie numerica, da 1 a 50 nella colonna A a partire dalla cella A7 (tale “colonna di servizio” verrà successivamente nascosta) mentre nella cella B7 è stata utilizzata la formula:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;$E$3*$E$4>=A7);A7;””)
La funzione SE, attraverso l’operatore logico E, verifica simultaneamente se le celle abilitate ad accogliere i dati iniziali non siano vuote e se il numero di rate complessive del prestito, dato dalla moltiplicazione della durata in anni per il numero di rate in un anno (E3*E4) è maggiore o uguale al numero contenuto nella cella A7 e restituisce, nel caso in cui il test si verifichi, quest’ultimo valore. La formula, ricopiata verso il basso fino alla cella B56, consente, pertanto, di visualizzare nella colonna B il numero progressivo delle rate del prestito mentre restituisce una cella vuota (le doppie virgolette dell’ultimo argomento della funzione SE) nelle celle restanti.
Per determinare le scadenze delle singole rate si è utilizzata la funzione DATA e, al suo interno, le funzioni ANNO, MESE e GIORNO. Analizziamole brevemente. La funzione DATA è composta da tre argomenti (rispettivamente, anno, mese e giorno) che vengono “riorganizzati” in formato data. Ad esempio la funzione =DATA(2007;12;31) restituisce la data 31/12/2007. La funzione è particolarmente utile per creare delle serie di dati ad intervalli regolari di giorni o di mesi, come nel modello che stiamo analizzando. Infatti, se l’argomento “giorno” supera i giorni del mese utilizzato come secondo argomento della funzione, l’eccedenza viene “traslata” sul mese successivo e, allo stesso, modo se il numero di mesi non trova capienza nell’anno (quindi, sono superiori a dodici), l’eccedenza viene traslata sull’anno successivo. Chiariamo con un esempio quanto esposto.
=> Piano di ammortamento di un mutuo con dati online in Excel
Consideriamo la funzione =DATA(2007;12;41); essendo dicembre composto da 31 giorni, i 10 giorni eccedenti vengono aggiunti al mese successivo ma poiché quest’ultimo supera il limite di 12 viene modificato automaticamente anche l’anno; il risultato della funzione sarà pertanto 10/01/2008. Le funzioni ANNO, MESE e GIORNO restituiscono rispettivamente l’anno il mese e il giorno di un numero seriale o di una data indicata come argomento. Supponiamo, ad esempio, di aver inserito la data 31/12/07 nella cella A1; la funzione =ANNO(A1) restituirà 2007, la funzione =MESE(A1) restituirà 12 mentre la funzione =GIORNO(A1) restituirà 31.
Torniamo al modello. Nella cella C7 è stata inserita (e poi copiata fino alla cella C56) la funzione:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;B7<>””);DATA(ANNO($G$3);MESE($G$3)+B7*12/$E$4;GIORNO($G$3));””).La funzione SE verifica, attraverso l’operatore logico E, che tutte le celle di input e la cella B7 contengano un valore (questa struttura verrà ripetuta anche per le formule successive e, pertanto, eviteremo di soffermarci nuovamente) e restituisce, il risultato della funzione DATA i cui argomenti fanno riferimento alla data del prestito inserita nella cella G3; da notare che l’argomento “mese” della funzione DATA (ovvero, MESE($G$3)+B7*12/$E$4) consente di calcolare il totale dei mesi complessivamente trascorsi dopo ogni rata e, quindi, di aggiornare automaticamente, attraverso il “meccanismo” della funzione DATA esaminato in precedenza, le singole date di scadenza.
Nella cella D7, per determinare la quota di capitale da rimborsare costantemente attraverso il pagamento delle singole rate si è utilizzata la formula:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;B7<>””);$C$3/($E$3*$E$4);””)
La formula, inserita sempre nella funzione SE e copiata successivamente fino alla cella D56, divide il capitale preso a prestito (C3) per il numero complessivo di rate (F3*F4).
La quota interessi di ogni singola rata si calcola moltiplicando il debito residuo per il tasso di interesse annuo per il numero di mesi della rata e dividendo il risultato conseguito per 12 (i mesi dell’anno). Per determinare la quota interessi relativa alla prima rata (cella E7) è stata utilizzata la formula:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;B7<>””);C3*C4/E4;””)
La formula moltiplica il prestito ottenuto (C3) per il tasso di interesse annuo (C4) e divide il risultato per il numero di rate in un anno (E4); da notare che quest’ultima divisione corrisponde, matematicamente, a moltiplicare per il numero di mesi della rata e a dividere per dodici. Nella cella E8 è stata utilizzata la formula:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;B8<>””);G7*$C$4/$E$4;””)
La funzione, successivamente copiata fino alla cella E56, ha una sintassi simile alla precedente ma fa riferimento al debito residuo indicato nella colonna G (nello specifico alla cella G7).
L’importo delle singole rate si calcola semplicemente sommando la quota capitale con la quota interessi; pertanto, nella cella F7 è stata trascritta, e successivamente copiata fino alla cella F56, la formula:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;B7<>””);D7+E7;””)
Per determinare il debito residuo in corrispondenza della prima rata, nella cella G7 è stata utilizzata la formula che esegue la differenza tra l’importo del prestito (C3) e la quota capitale versata con la prima rata (D7).:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;B7<>””);C3-D7;””)
Per calcolare il debito residuo in corrispondenza della seconda rata è stata utilizzata nella cella G8 la formula che esegue la differenza tra il debito residuo dopo il versamento della prima rata (G7) e la quota capitale della seconda rata (D8); la funzione è stata copiata, infine, fino alla cella G56:
=SE(E($C$3<>””;$C$4<>””;$E$3<>””;$E$4<>””;$G$3<>””;B8<>””);G7-D8;””)
=> Piano di ammortamento prestiti con Excel
Poiché la struttura delle funzioni SE utilizzate prevede la restituzione di una “etichetta vuota” nel caso in cui non si utilizzino le righe del piano di ammortamento del prestito, e poiché quest’ultimo è stato costruito senza una riga dei totali, si è utilizzata la formattazione condizionale per formattare con dei bordi soltanto le celle contenenti un valore; quest’ultimo accorgimento consente di visualizzare il prospetto in maniera compatta.
Si è selezionato, pertanto, l’intervallo B7:G56, si è utilizzato il comando Formattazione condizionale disponibile nel menu Formato, si è impostata come condizione la formula con riferimento misto =$B7<>”” (la formula è stata costruita con riferimento misto per assegnare simultaneamente il formato a tutte le celle dell’intervallo) e, attraverso il pulsante Formato, si è intervenuti all’interno della finestra Formato celle per assegnare un bordo alle celle dell’intervallo.

Come personalizzare il modello
Il modello è stato costruito prevedendo un massimo di cinquanta rate; nel caso in cui si deve procedere alla creazione di un piano di ammortamento con rate maggiori è sufficiente selezionare l’intervallo A56:G56 (dopo aver visualizzato la colonna nascosta A) e copiare verso il basso con il quadratino di riempimento.









