
Dopo aver spiegato in precedenti tutorial come valutare la convenienza finanziaria tra due o più investimenti alternativi, considerando un tasso di attualizzazione o anche senza necessità di stimarlo, vediamo in questo articolo come applicare queste funzioni nelle scelte strategiche.
Facciamo ricorso ad alcuni esempi pratici in excel da scaricare e personalizzare.
Investimenti alternativi: tassi di interesse a confronto
Da un punto di vista matematico, la funzione TASSO di Excel ci restituisce il tasso di interesse che rende uguale a zero il Valore Attuale di una serie di flussi di cassa. Tra due o più investimenti alternativi è da preferire, come illustreremo in seguito, quello che ha un tasso maggiore.
La funzione, costituita da sei argomenti, ha la seguente sintassi:
=TASSO(periodi;pagamento;val_attuale;val_futuro;tipo;ipotesi)
- L’argomento periodi è dato dal numero totale dei pagamenti, mentre l’argomento pagamento è dato dal flusso di cassa costante pagato o riscosso in ogni periodo.
- L’argomento val_attuale indica, il flusso di cassa pagato o riscosso al periodo iniziale (periodo 0). L’argomento valore_futuro è dato dal flusso di cassa eventuale relativo all’ultimo periodo in aggiunta al valore del pagamento.
Come si calcola il tasso di attualizzazione di un investimento
L’argomento tipo, indica il tempo nel quale vengono generati i flussi di cassa: un valore pari a uno (1) indica che gli importi dei flussi di cassa sono generati all’inizio dei singoli periodi, mentre un valore pari a zero (0) o la sua omissione, indica che i flussi si riferiscono alla fine dei singoli periodi.
Infine, l’argomento ipotesi è il tasso con il quale Excel inizia il procedimento di calcolo interattivo che consente di individuare il tasso che rende pari a zero il Valore Attuale dei flussi di cassa indicati negli altri argomenti della funzione (se viene omesso Excel inizia con un tasso di interesse uguale a 0,1).
La funzione TASSO richiede una attenta valutazione dei segni algebrici da utilizzare per i suoi argomenti in quanto può essere impiegata, come la maggior parte delle funzioni finanziarie, sia per la valutazione degli investimenti che dei finanziamenti.
Nella nostra ipotesi, trattandosi di investimenti, l’argomento pagamento deve essere indicato con il segno positivo in quanto sono flussi di cassa generati dall’investimento, mentre, l’esborso necessario per acquisire l’investimento, corrispondente all’argomento val_attuale, va indicato con il segno negativo; infine, l’argomento val_futuro, che indica il flusso di cassa riscosso per l’eventuale vendita del bene strumentale dopo il suo utilizzo, va indicato, ancora una volta, con segno positivo.
Inoltre, se l’argomento periodi non è riferito ad annualità (ad esempio, nel caso in cui si attualizzano flussi di cassa semestrali o quadrimestrali) occorre tenere presente che il risultato della funzione TASSO esprime il tasso periodico e, di conseguenza, va eguagliato all’annualità (riprendendo l’esempio, sarà necessario moltiplicare il risultato per 2 nel caso di flussi semestrali o per 3 nel caso di flussi quadrimestrali).
Modelli di esempio da scaricare
Utilizziamo due esempi pratici per approfondire la conoscenza della funzione TASSO e le sue relazioni con la funzione VA.
1° esempio: acquisto impianti a confronto
Supponiamo che l’impianto A costi 240.000 € e consente di realizzare prodotti dalla cui vendita si ottengano introiti netti annui costanti pari a 70.000 €, mentre l’impianto B costi 300.000 € e genera, a seguito della maggiore capacità produttiva, flussi di cassa annuali pari a 80.000 €.
Supponiamo, inoltre, che al termine del sesto anno l’impianto A possa essere dismesso recuperando 20.000 € mentre dalla vendita dell’impianto B si ottenga 40.000 €.
Determiniamo, attraverso l’utilizzo della funzione TASSO, quale tra i due investimenti è da considerarsi conveniente dal punto di vista finanziario. Trasferiamo i dati su di un foglio di calcolo come rappresentato in figura.
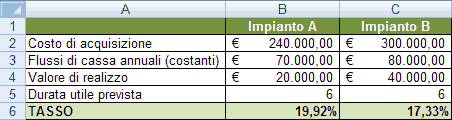
Per determinare il tasso che rende pari a zero il Valore Attuale dell’Impianto A, abbiamo utilizzato nella cella B6 la formula: =TASSO(B5;B3;-B2;B4)
Il primo argomento della funzione (B5) indica la durata dell’investimento, il secondo (B3) i flussi di cassa positivi generati dall’investimento, il terzo argomento è stato trascritto con segno meno (-B2) in quanto indica l’esborso iniziale per l’acquisto dell’Impianto A, ed infine, il quarto argomento indica il presunto valore di realizzo (B4) al termine del sesto anno (indicato con segno positivo in quanto si tratta di un introito monetario).
L’argomento tipo è stato omesso in quanto si ipotizzano flussi di cassa posticipati mentre l’argomento ipotesi è stato omesso per lasciare ad Excel il compito di trovare una soluzione attraverso il calcolo interattivo.
La funzione è stata successivamente copiata per trascinamento nella cella C6. Dal risultato delle funzioni TASSO si evince che l’Impianto A è da preferire all’Impianto B in quanto ha un risultato percentuale maggiore. Cerchiamo di spiegare finanziariamente quest’ultima affermazione.
Se si calcola il Valore Attuale (attraverso la funzione VA) dei flussi di cassa dell’Impianto A applicando un tasso di attualizzazione del 19,92%, si ottiene un valore pari a 240.000 € che sommato algebricamente al costo di acquisizione dell’impianto da come risultato zero (0).
Proviamo a verificare quanto affermato.La funzione VA ha la seguente sintassi:
=VA(tasso_int;periodi;pagamento;valore_futuro;tipo)
Trascriviamo la funzione VA in una qualsiasi cella del foglio di calcolo ed utilizziamo come primo argomento della funzione il risultato della funzione TASSO, nel modo seguente:
=-VA(B6;B5;B3;B4)
Il risultato che otteniamo è 240.000 € pari, appunto all’esborso iniziale per l’acquisto dell’Impianto A. Allo stesso modo, se si applica un tasso di attualizzazione del 17,33% per attualizzare i flussi di cassa relativi all’Impianto B, si ottiene come risultato della funzione VA un valore pari a 300.000 € che consente di azzerare (considerando l’esborso iniziale) il Valore Attuale dell’investimento.
Detto in altri termini, se si ipotizza un tasso di attualizzazione del 17,33%, l’investimento nell’Impianto B non genera “utili“.
Proviamo ora ad utilizzare, anche per l’Impianto A, quest’ultimo tasso di attualizzazione trascrivendo in una qualsiasi cella del foglio di calcolo la funzione:
=-VA(C6;B5;B3;B4)
Il risultato che si ottiene (256.751 €) indica che, ad un tasso del 17,33%, l’investimento nell’Impianto A genera flussi positivi pari a 16.751 € (256.751 € – 240.000 €) e, pertanto, è da preferire all’Impianto B che non genera alcun flusso.
La dimostrazione della convenienza dell’investimento nell’Impianto A (e più in generale, dell’investimento che ha un tasso maggiore) poteva essere fatta anche utilizzando il tasso di attualizzazione dell’Impianto A: in questo caso, avremmo ottenuto che ad un tasso di attualizzazione del 19,92%, l’investimento nell’Impianto A non generava alcun “utile”, mentre quello nell’Impianto B generava una perdita.
2° esempio: stipula contratti a confronto
Supponiamo di acquistare un bene da dare in locazione del valore di 100.000 € e di voler determinare quale dei due contratti di locazione (Contratto A e B) è più conveniente dal punto di vista finanziario.
Il contratto A prevede la riscossione di un canone di locazione semestrale anticipato del valore di 10.000 € ed ha una durata di 7 anni. Il contratto B prevede la riscossione di canoni trimestrali, sempre anticipati, del valore di 6.500 € ed ha una durata di 5 anni; inoltre, in questa seconda ipotesi è prevista la possibilità di vendere il bene non completamente usurato e di ottenere un valore di realizzo pari a 10.000 €.
Trasferiamo i dati su di un foglio di calcolo come rappresentato in figura.
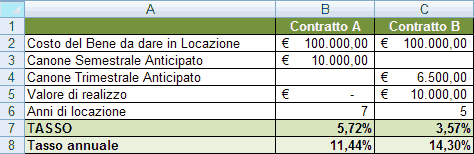
Per determinare il tasso che rende il Valore Attuale del Contratto A pari a zero possiamo utilizzare nella cella B7 la funzione: =TASSO(B6*2;B3;-B2;;1)
L’argomento periodi è stato ottenuto moltiplicando per due (2) il valore della cella B6 in quanto i canoni di locazione sono di tipo semestrale; l’argomento pagamento è dato dal canone di locazione riscosso semestralmente (B3); inoltre, poiché quest’ultimo viene pagato anticipatamente, abbiamo utilizzato 1 come argomento tipo della funzione (da notare il doppio punto e virgola che consente di “saltare” l’argomento val_futuro); abbiamo, infine, omesso l’argomento ipotesi.
Una formula analoga è stata utilizzata per determinare il TASSO relativo al Contratto B:
=TASSO(C6*4;C4;-C2;C5;1)
In questa seconda formula, poiché i canoni sono riscossi trimestralmente, i periodi sono stati calcolati moltiplicando per quattro (4) il valore della cella C6. Infine, per individuare la convenienza tra le due ipotesi alternative è stato necessario “eguagliare” i due valori ottenuti dalla funzione TASSO; pertanto, nella cella B8 si è moltiplicato per due il tasso “semestrale” calcolato nella cella B7, mentre nella cella C8 si è moltiplicato per quattro il tasso “trimestrale” ottenuto nella cella C7.
Poiché il valore contenuto nella cella C8 è maggiore di quello della cella B8, possiamo affermare che, finanziariamente, il Contratto B è da preferire al Contratto A (da notare che un solo calcolo algebrico avrebbe portato a ritenere “indifferente” la scelta tra i due investimenti in quanto entrambi i contratti generano entrate per 140.000 &;euro;!).
di Corrado del Buono








